ฟังก์ชันขั้นบันได

ฟังก์ชันขั้นบันได หมายถึง ฟังก์ชันที่มีโดเมนเป็นสับเซตของเซตของจำนวนจริง และมีค่าของฟังก์ชันเป็นค่าคงตัวเป็นช่วงๆ มากกว่าสองช่วง กราฟจะมีลักษณะคล้ายขั้นบันได. 

อ่านเพิ่มเติม

ฟังก์ชันค่าสัมบูรณ์

ฟังก์ชันค่าสัมบูรณ์

ฟังก์ชันค่าสมบูรณ์ถูกกำหนดโดยกฎซึ่งแบ่งออกเป็นสองกรณี

ค่าฟังก์ชันสมบูรณ์ | | จะกำหนดโดย


ค่า absolute ของ x ให้ระยะห่างระหว่าง x และ 0 เป็นบวกหรือศูนย์เสมอ

ตัวอย่างเช่น

|3| = 3, |-3| = 3, |0|=0. | 3 | = 3, | -3 | = 3 | 0 | = 0

โดเมนของฟังก์ชันค่าสมบูรณ์คือ R ทั้งเส้นของจริงในขณะที่ช่วงคือช่วง [0, ∞)

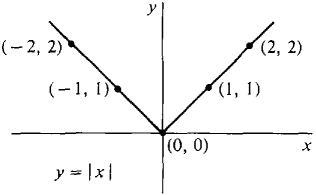
ฟังก์ชันค่าสมบูรณ์สามารถอธิบายกฎ

กราฟมันจะได้รับโดยสมการ y =  กราฟเป็น V แสดงในรูปที่ 1.2.10

 อ่านเพิ่มเติม

ฟังก์ชันเอกซ์โพเนนเชียล

ฟังก์ชันนั้นมีอยู่หลายรูปแบบ แต่ละแบบก็มีการตั้งชื่อไม่เหมือนกัน ฟังก์ชันเอกซ์โพเนนเชียลก็เป็นอีกรูปแบบหนึ่งของฟังก์ชันซึ่งเราจะไปดูว่าฟังก์ชันเอกซ์โพนเนนเชียลนั้นมีรูปแบบอย่างไร ก็ต้องไปดูนิยามของมันครับ ว่านิยามของฟังก์ชันเอกซ์โพเนนเชียลนั้นเป็นอย่างไร

นิยาม ฟังก์ชันเอ็กซ์โพเนนเชียลคือ ฟังก์ชัน

จากบทนิยามของฟังก์ชันเอกซ์โพเนนเชียล ฟังก์ชันนี้มีรูปแบบในรูปของเลขยกกำลัง โดยฐานของมันต้องมากกว่า 0 และฐานต้องไม่เป็น 1  ตัวอย่างของฟังก์ชันเอกซ์โพเนนเชียลเช่น อ่านเพิ่มเติม

ฟังก์ชันกำลังสอง

ฟังก์ชันกำลังสอง   (Quadratic function)

           

ฟังก์ชันกำลังสองเป็นฟังก์ชันที่อยู่ในรูป    y   =   ax2 + bx + c   เมื่อ  a, b, c  เป็นจำนวนจริงใด ๆ  และ  a ¹ 0   ซึ่งกราฟของฟังก์ชันกำลังสอง  เรียกว่า  พาราโบลา
1)     y  =  2x2 + 3x – 10     เมื่อ   a = 2 ,  b = 3   และ  c = -1
                                2)     y  =   x2 + 1                เมื่อ   a = 1 ,  b = 0   และ  c =  1
                                3)     y  =  -x2 + 2x + 1       เมื่อ   a = -1 ,  b = 2   และ  c = 1
                1)   กราฟของฟังก์ชันกำลังสอง ที่กำหนดด้วยสมการ    y  =  ax2   เมื่อ  a ¹ 0
                         กราฟของฟังก์ชันกำลังสอง   มีชื่อเรียกว่า  พาราโบลา  ซึ่งลักษณะของกราฟของฟังก์ชันขึ้นอยู่กับค่าของ  a , b  และ  c   และเมื่อ  a  เป็นบวกหรือลบ  จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ  และกราฟของฟังก์ชันกำลังสองที่กำหนดด้วยสมการ    y  =  ax2   เมื่อ  a ¹ 0       เมื่อ  a  > 0   และชนิดคว่ำ   เมื่อ   a < 0    อ่านเพิ่มเติม

ฟังก์ชันเชิงเส้น

 ฟังก์ชันเชิงเส้น   คือ ฟังก์ชันที่อยู่ในรูป y = ax+b เมื่อ a ,b เป็นจำนวนจริง และ  กราฟของฟังก์ชันเชิงเส้นจะเป็นเส้นตรง

ฟังก์ชัน  y  =  ax + b  เมื่อ    a  =  0  จะได้ฟังก์ชันที่อยู่ในรูป  y  =  b  ซึ่งมีชื่อเรียกว่า  ฟังก์ชันคงตัว  (constant  function)  กราฟของฟังก์ชันคงตัวจะเป็นเส้นตรงที่ขนานกับแกน  X  ตัวอย่างของฟังก์ชันคงตัว  ได้แก่  อ่านเพิ่มเติม

ความสัมพันธ์และฟังก์ชัน

คู่อันดับ (Order Pair) เป็นการจับคู่สิ่งของโดยถือลำดับเป็นสำคัญ เช่น คู่อันดับ a, b จะเขียนแทนด้วย (a, b) เรียก a ว่าเป็นสมาชิกตัวหน้า และเรียก b ว่าเป็นสมาชิกตัวหลัง
(การเท่ากับของคู่อันดับ) (a, b) = (c, d) ก็ต่อเมื่อ a = c และ b = d
ผลคูณคาร์ทีเชียน (Cartesian Product) ผลคูณคาร์ทีเซียนของเซต A และเซต B คือ เซตของคู่อันดับ (a, b) ทั้งหมด โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B
สัญลักษณ์      ผลคูณคาร์ทีเซียนของเซต A และเซต B เขียนแทนด้วย A x Bหรือ เขียนในรูปเซตแบบบอกเงื่อนไขจะได้ว่า 
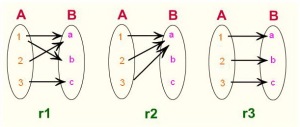
ความสัมพันธ์ (Relation)
r เป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ A x B อ่านเพิ่มเติม

ค่าสัมบูรณ์ของจำนวนจริง

ค่าสัมบูรณ์ของจำนวนจริง a ใดๆ เขียนแทนด้วย |a| หมายถึง ระยะทางจากจุด 0 จนถึงจุด บนเส้นจำนวน ตัวอย่างเช่นเนื่องจากระยะทางต้องมีค่าเป็นจำนวนจริงบวกหรือศูนย์ ดังนั้น บทนิยามของค่าสัมบูรณ์สามารถเขียนได้ดังนี้

บทนิยาม

สำหรับจำนวนจริง x ทุกตัว ค่าสัมบูรณ์ของ x ทฤษฎีบทเกี่ยวกับค่าสัมบูรณ์

 1. |x| = a ก็ต่อเมื่อ x = a หรือ x = -a

 2. |x| = |-x|

 3. |x| = |y| ก็ต่อเมื่อ x = y หรือ x = -y

 4. |x| = √x2

5. |x| ≥ 0

6. |x| ≥ x

7. |xy| = |x| |y|

8. |x/y| = |x|/|y|

9. |x - y| = |y - x|

10. |x2| = |x|2 = x2

11. |x + y| = |x| + |y| ก็ต่อเมื่อ xy ≥ 0

12. |x| ≤ a ก็ต่อเมื่อ -a ≤ x ≤ a

13. |x| ≥ a ก็ต่อเมื่อ  x ≤ -a หรือ x ≥ a

14. |x + y| ≤ |x| + |y|

15. |x - y| ≥ |x| - |y|  อ่านเพิ่มเติม

สมบัติของการไม่เท่ากัน

สมบัติของการไม่เท่ากัน

  กำหนดให้ a, b, c เป็นจำนวนจริงใดๆ

              1. สมบัติการถ่ายทอด     ถ้า a > b และ b > c แล้ว a > c  
 
      2. สมบัติการบวกด้วยจำนวนที่เท่ากัน ถ้า a > b แล้ว a + c > b+ c
 
      3. จำนวนจริงบวกและจำนวนจริงลบ
            a เป็นจำนวนจริงบวก ก็ต่อเมื่อ a > 0
            a เป็นจำนวนจริงลบ ก็ต่อเมื่อ a < 0

      4. สมบัติการคูณด้วยจำนวนเท่ากันที่ไม่เท่ากับศูนย์
            ถ้า a > b และ c > 0 แล้ว ac > bc
            ถ้า a > b และ c < 0 แล้ว ac < bc

      5. สมบัติการตัดออกสำหรับการบวก ถ้า a + c > b + c แล้ว a > b

      6. สมบัติการตัดออกสำหรับการคูณ
            ถ้า ac > bc และ c > 0 แล้ว a > b
            ถ้า ac > bc และ c < 0 แล้ว a < b  อ่านเพิ่มเติม

การนำสมบัติของจำนวนจริงไปใช้ในการเเก้สมการกำลังสอง

จำนวนจริง

เซตของจำนวนจริงประกอบด้วยสับเซตที่สำคัญ  ได้แก่
- เซตของจำนวนนับ/ เซตของจำนวนเต็มบวก เขียนแทนด้วย  I
                   I = {1,2,3…}
- เซตของจำนวนเต็มลบ  เขียนแทนด้วย  I
- เซตของจำนวนเต็ม เขียนแทนด้วย I
                   I = { …,-3,-2,-1,0,1,2,3…}
- เซตของจำนวนตรรกยะ : เซตของจำนวนจริงที่สามารถเขียนได้ในรูปเศษส่วน      โดยที่ a,b เป็นจำนวนเต็ม  และ b = 0  อ่านเพิ่มเติม

สมบัติของจำนวนจริงเกี่ยวกับการบวกและการคูณ

จำนวนจริง

จำนวนตรรกยะ (rational number) เป็นจำนวนจริงที่สามารถเขียนได้ในรูปเศษส่วนของจำนวนเต็มที่ตัวส่วนไม่เป็นศูนย์ และเขียนในรูปทศนิยมซ้ำได้

จำนวนอตรรกยะ (irrational number) เป็นจำนวนจริงที่ไม่ใช่จำนวนตรรกยะซึ่งไม่สามารถเขียนในรูปทศนิยมซ้ำหรือเศษส่วนของจำนวนเต็มที่ตัวส่วนไม่เป็นศูนย์แต่เขียนได้ในรูปทศนิยมไม่ซ้ำ และ

สามารถกำหนดค่าโดยประมาณได้

การเขียนเศษส่วนในรูปทศนิยม คือ การนำส่วนไปหารเศษ

การเขียนทศนิยมในรูปเศษส่วน คือ ทศนิยม 1 ตำแหน่ง หารด้วย 10 2 ตำแหน่งหาร 100 ไปเรื่อยๆๆๆๆ แต่ถ้าเป็นทศนิยมซ้ำ ใช้วิธีลัด เช่น 0.45• = 45-4/90 = 41/90  อ่านเพิ่มเติม

ระบบจำนวนจริง

• ระบบจำนวนจริง
จากแผนผังแสดงความสัมพันธ์ของจำนวนข้างต้น จะพบว่า ระบบจำนวนจริง จะประกอบไปด้วย

1. จำนวนอตรรกยะ หมายถึง จำนวนที่ไม่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็ม หรือทศนิยมซ้ำได้ ตัวอย่างเช่น √2 , √3, √5, -√2, - √3, -√5 หรือ ¶ ซึ่งมีค่า 3.14159265...

2. จำนวนตรรกยะ หมายถึง จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็มหรือทศนิยมซ้ำได้ ตัวอย่างเช่น อ่านเพิ่มเติม

การให้เหตุผลแบบนิรนัย

การให้เหตุผลแบบนิรนัย

               

การให้เหตุผลแบบนิรนัยเป็นวิธีการให้เหตุผลโดยสรุปผลจากข้อความซึ่งเป็นความจริงทั่วไปมาเป็นข้ออ้างเพื่อสนับสนุนให้เกิดข้อสรุปที่เป็นความรู้ใหม่ที่เป็นข้อสรุปส่วนย่อยข้อสรุปที่ได้จากการให้เหตุผล

แบบนิรนัยนั้นจะเป็นข้อสรุปที่อยู่ในขอบเขตของเหตุเท่านั้นจะเป็นข้อสรุปที่กว้างหรือเกินกว่าเหตุไม่ได้การให้เหตุผลแบบนิรนัยประกอบด้วยข้อความ2กลุ่มโดยข้อความกลุ่มแรกเป็นข้อความที่เป็นเหตุ เหตุอาจมี

หลาย ๆเหตุ หลาย ๆข้อความ และข้อความกลุ่มที่สองจะเป็นข้อสรุป ข้อความในกลุ่มแรกและกลุ่มที่สองจะต้องมีความสัมพันธ์กัน อ่านเพิ่มเติม

การให้เหตุผลแบบอุปนัย

การให้เหตุผลแบบอุปนัย (Inductive Reasoning)

เกิดจากการที่มีสมมติฐานกรณีเฉพาะ หรือเหตุย่อยหลายๆ เหตุ เหตุย่อยแต่ละเหตุเป็นอิสระจากกัน มีความสำคัญเท่าๆ กัน และเหตุทั้งหลายเหล่านี้ไม่มีเหตุใดเหตุหนึ่งแสดงให้เห็นถึงความเป็นสมมติฐานกรณีทั่วไป หรือกล่าวได้ว่า การให้เหตุผลแบบอุปนัยคือการนำเหตุย่อยๆ แต่ละเหตุมารวมกัน เพื่อนำไปสู่ผลสรุปเป็นกรณีทั่วไป เช่นตัวอย่างการให้เหตุผลแบบอุปนัย อ่านเพิ่มเติม

ยูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต

ยูเนียน (Union)

ยูเนียน (Union) มีนิยามว่า เซต A ยูเนียนกับเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ เซต B หรือทั้ง A และ B สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B

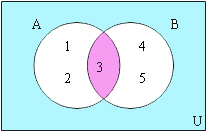
อินเตอร์เซกชัน (Intersection)

อินเตอร์เซกชัน (Intersection) มีนิยามคือ เซต A อินเตอร์เซกชันเซต B คือ เซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B

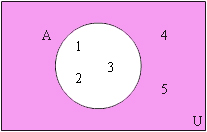
คอมพลีเมนต์ (Complements) 

มีนิยามคือ ถ้าเซต A ใดๆ ในเอกภพสัมพัทธ์ U แล้วคอมพลีเมนต์ของเซต A คือ เซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่เป็นสมาชิกของ A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A’  อ่านเพิ่มเติม

สับเซตและเพาเวอร์เซต

สับเซตและเพาเวอร์เซต

• สับเซต
บทนิยาม เซต A เป็นสับเซตของเซต B ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B และสามารถเขียนแทนได้ด้วยสัญลักษณ์ A ⊂B
ตัวอย่างที่ 1 A = {1, 2, 3}
B = { 1, 2, 3, 4, 5}
∴ A ⊂ B

• เพาเวอร์เซต
บทนิยาม เพาเวอร์เซตของเซต A คือ เซตซึ่งประกอบด้วยสมาชิกที่เป็นสับเซตทั้งหมดของเซต A และสามารถเขียนแทนได้ด้วยสัญลักษณ์ P(A)
ตัวอย่างที่ 1 A = Ø
สับเซตทั้งหมดของ A คือ Ø
∴ P(A) = {Ø }
ตัวอย่างที่ 2 B = {1}
สับเซตทั้งหมดของ B คือ Ø, {1}
∴ P(B) = {Ø, {1} }
ตัวอย่างที่ 3 C = {1,2}
สับเซตทั้งหมดของ C คือ Ø, {1} , {2}, {1,2}
∴ P(C) ={Ø, {1} , {2}, {1,2} }  อ่านเพิ่มเติม

เอกภพสัมพัทธ์

เอกภพสัมพัทธ์ คือ เซตที่ประกอบด้วยสมาชิกทั้งหมดของสิ่งที่เราต้องการจะศึกษา สามารถเขียนแทนได้ด้วยสัญลักษณ์ u
           เอกภพสัมพัทธ์ (Relative Universe) ในการพูดถึงเรื่องใดก็ตามในแง่ของเซต  เรามักมีขอบข่ายในการพิจารณาสมาชิกของเซตที่จะกล่าวถึง  โดยมีข้อตกลงว่าเราจะไม่กล่าวถึงสิ่งใดนอกเหนือไปจากสมาชิก ของเซตที่กำหนดขึ้น เช่น ถ้าเรากำหนดเซตของสมาชิกทุกคนในครอบครัวของผู้เรียนเองให้เป็นเซตใหญ่ที่สุด  เราจะเรียกเซตนี้ว่า เอกภพสัมพัทธ์   เขียนแทนด้วยสัญลักษณ์  U โดยมีข้อตกลงว่า เมื่อกล่าวถึงสมาชิกของเซตใด ๆ จะไม่กล่าวถึงสิ่งอื่นที่นอกเหนือจากสมาชิกในเอกภพสัมพัทธ์  อ่านเพิ่มเติม

เซต

1 เซต

เซต  เป็นคำที่ใช้บ่งบอกถึงกลุ่มของสิ่งต่างๆ และเมื่อกล่าวถึงกลุ่มใดแน่นอนว่าสิ่งใดอยู่ในกลุ่ม สิ่งใดไม่อยู่ในกลุ่ม เช่น

       เซตสระในภาษาอังกฤษ  หมายถึง  กลุ่มของอังกฤษ  a, e, i, o และ u

       เซตของจำนวนนับที่น้อยกว่า 10 หมายถึง  กลุ่มตัวเลข 1,2,3,4,5,6,7,8,และ9

        สิ่งที่ในเชตเรียกว่า  สมาชิก  ( element หรือ members )  อ่านเพิ่มเติม